Classic VRPs¶
This notebook shows how to use PyVRP to solve two classic variants of the VRP: the capacitated vehicle routing problem (CVRP), and the vehicle routing problem with time windows (VRPTW). It builds on the tutorial by solving much larger instances, and going into more detail about the various plotting tools and diagnostics available in PyVRP.
A CVRP instance is defined on a complete graph \(G=(V,A)\), where \(V\) is the vertex set and \(A\) is the arc set. The vertex set \(V\) is partitioned into \(V=\{0\} \cup V_c\), where \(0\) represents the depot and \(V_c=\{1, \dots, n\}\) denotes the set of \(n\) customers. Each arc \((i, j) \in A\) has a weight \(d_{ij} \ge 0\) that represents the travel distance from \(i \in V\) to \(j \in V\). Each customer \(i \in V_c\) has a demand \(q_{i} \ge 0\). The objective is to find a feasible solution that minimises the total distance.
A VRPTW instance additionally incorporates time aspects into the problem. For the sake of exposition we assume the travel duration \(t_{ij} \ge 0\) is equal to the travel distance \(d_{ij}\) in this notebook. Each customer \(i \in V_c\) has a service time \(s_{i} \ge 0\) and a (hard) time window \(\left[e_i, l_i\right]\) that denotes the earliest and latest time that service can start. A vehicle is allowed to arrive at a customer location before the beginning of the time window, but it must wait for the window to open to start the delivery. Each vehicle must return to the depot before the end of the depot time window \(H\). The objective is to find a feasible solution that minimises the total distance.
Let’s first import what we will use in this notebook.
[1]:
import matplotlib.pyplot as plt
from tabulate import tabulate
from vrplib import read_solution
from pyvrp import Model, read
from pyvrp.plotting import (
plot_coordinates,
plot_instance,
plot_result,
plot_route_schedule,
)
from pyvrp.stop import MaxIterations, MaxRuntime
The capacitated VRP¶
Reading the instance¶
We will solve the X-n439-k37 instance, which is part of the X instance set that is widely used to benchmark CVRP algorithms. The function pyvrp.read reads the instance file and converts it to a ProblemData instance. We pass the argument round_func="round" to compute the Euclidean distances rounded to the nearest integral, which is the convention for the X benchmark set. We also load the best known solution to
evaluate our solver later on.
[2]:
INSTANCE = read("data/X-n439-k37.vrp", round_func="round")
BKS = read_solution("data/X-n439-k37.sol")
Let’s plot the instance and see what we have.
[3]:
_, ax = plt.subplots(figsize=(8, 8))
plot_coordinates(INSTANCE, ax=ax)
plt.tight_layout()
Solving the instance¶
We will again use the Model interface to solve the instance. The Model interface supports a convenient from_data method that can be used to instantiate a model from a known ProblemData object.
[4]:
model = Model.from_data(INSTANCE)
result = model.solve(stop=MaxIterations(2000), seed=42)
print(result)
Solution results
================
# routes: 37
# clients: 438
objective: 36661.00
# iterations: 2000
run-time: 33.23 seconds
Routes
------
Route #1: 348 411 3 169 2 8 311 434 105 236 217 414
Route #2: 370 133 425 349 223 299 386 267 400 97 410 72
Route #3: 353 195 202 308 270 406 155 41 275 92 260 26
Route #4: 250 206 418 122 145 200 139 392 57 296 375 281
Route #5: 71 228 346 162 435 166 345 385 438 312 381 404
Route #6: 280 245 110 409 421 211 347 43 218 239 42 335
Route #7: 324 229 268 227 221 342 360 393 237 121 325 249
Route #8: 437 44 422 149 172 326
Route #9: 241 303 225 388 83 66 126 297 86 315 352 264
Route #10: 233 420 396 423 391 372 242 337 433 377 380 115
Route #11: 339 293 89 412 407 416 366 384 403 17 428 402
Route #12: 383 257 253 289 271 338 266 351 432 413 321 243
Route #13: 329 319 309 252 101 285 193 215 153 15 159 65
Route #14: 251 137 98 341 350 286 47 376 138 246 323 283
Route #15: 25 334 144 431 197 7 344 80 130 61 189 79
Route #16: 176 131 6 56 22 210 88 173 118 91 154 146
Route #17: 62 371 109 90 113 116 274 196 75 140 1 367
Route #18: 204 31 5 426 134 397 390 184 395 287 387 207
Route #19: 333 58 161 361 220 331 330 19 248 430 28 401
Route #20: 108 340 240 408 302 255 152 327 389 343 24 175
Route #21: 132 4 34 230 378 112 16 67 177 135 157 73
Route #22: 84 181 21 11 209 354 74 63 117 103 13 244
Route #23: 265 313 178 310 222 125 190 356 290 368 417 399
Route #24: 124 99 216 106 183 170 182 78 256 96 179 81
Route #25: 234 95 168 272 123 64 10 37 301 379 394 171
Route #26: 77 364 259 30 291 160 292 174 382 192 235 165
Route #27: 424 300 363 357 214 198 52 328 213 279 114 316
Route #28: 332 120 269 284 282 150 205 219 142 151 163 53
Route #29: 199 39 232 336 304 419 405 369 188 320 273 224
Route #30: 128 186 54 27 100 141 208 374 322 35 51 164
Route #31: 48 12 85 69 68 111 20 148 314 306 107 180
Route #32: 38 167 203 247 201 40 46 212 94 49 45 277
Route #33: 93 258 70 129 191 158 29 87 102 127 119 76
Route #34: 194 50 18 307 262 261 14 436 373 36 427 156
Route #35: 254 9 295 358 359 365 429 355 276 317 398 415
Route #36: 263 55 23 318 294 185 104 60 143 147 82 32
Route #37: 226 278 33 298 288 238 305 362 187 136 59 231
[5]:
gap = 100 * (result.cost() - BKS["cost"]) / BKS["cost"]
print(f"Found a solution with cost: {result.cost()}.")
print(f"This is {gap:.1f}% worse than the best known", end=" ")
print(f"solution, which is {BKS['cost']}.")
Found a solution with cost: 36661.
This is 0.7% worse than the best known solution, which is 36391.
We’ve managed to find a very good solution quickly!
The Result object also contains useful statistics about the optimisation. We can now plot these statistics as well as the final solution use plot_result.
[6]:
fig = plt.figure(figsize=(15, 9))
plot_result(result, INSTANCE, fig)
fig.tight_layout()
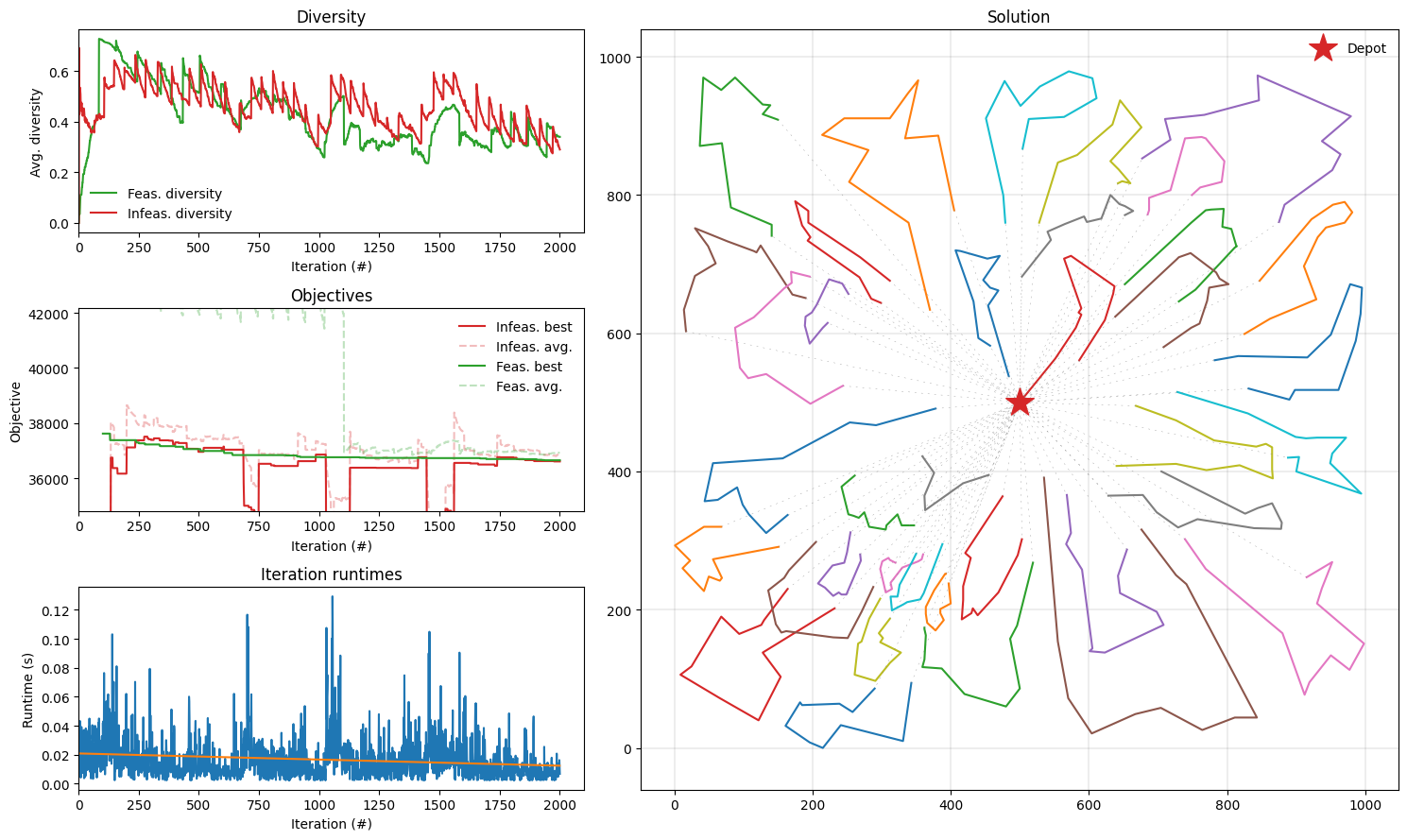
PyVRP internally uses a genetic algorithm consisting of a population of feasible and infeasible solutions. These solutions are iteratively combined into new offspring solutions, that should result in increasingly better solutions. Of course, the solutions should not all be too similar: then there is little to gain from combining different solutions. The top-left Diversity plot tracks the average diversity of solutions in each of the feasible and infeasible solution populations. The Objectives plot gives an overview of the best and average solution quality in the current population. The bottom-left figure shows iteration runtimes in seconds. Finally, the Solution plot shows the best observed solution.
The VRP with time windows¶
Reading the instance¶
We start with a basic example that loads an instance and solves it using the standard configuration used by the Model interface. For the basic example we use one of the well-known Solomon instances.
We again use the function pyvrp.read. We pass the following arguments:
instance_format="solomon": this parses the instance file as a Solomon formatted instance.round_func="trunc1": following the DIMACS VRP challenge convention, this computes distances and durations truncated to one decimal place.
[7]:
INSTANCE = read(
"data/RC208.vrp",
instance_format="solomon",
round_func="trunc1",
)
BKS = read_solution("data/RC208.sol")
Let’s plot the instance and see what we have. The function plot_instance will plot time windows, demands and coordinates, which should give us a good impression of what the instance looks like. These plots can also be produced separately by calling the appropriate plot_* function: see the API documentation for details.
[8]:
fig = plt.figure(figsize=(12, 6))
plot_instance(INSTANCE, fig)
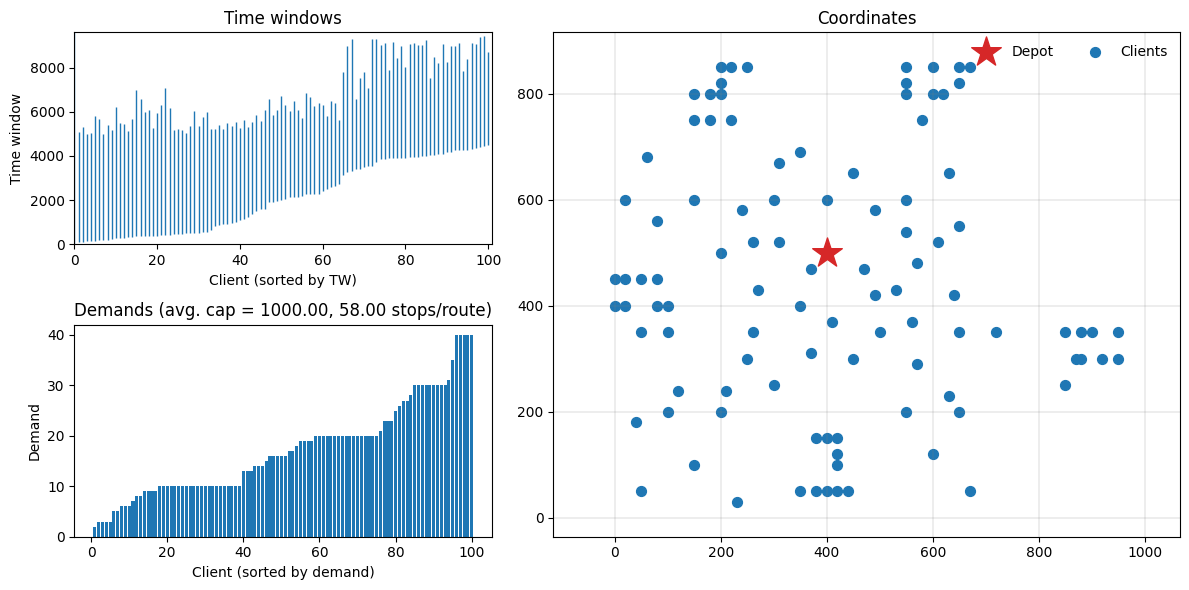
Solving the instance¶
We will again use the Model interface to solve the instance.
[9]:
model = Model.from_data(INSTANCE)
result = model.solve(stop=MaxIterations(1000), seed=42)
print(result)
Solution results
================
# routes: 5
# clients: 100
objective: 7812.00
# iterations: 1000
run-time: 1.78 seconds
Routes
------
Route #1: 90 82 99 52 9 10 11 13 15 16 17 47 14 12 53
Route #2: 65 83 64 49 19 18 48 21 23 25 77 58 75 97 59 87 74 86 57 24 22 20 66
Route #3: 94 92 95 67 62 50 34 31 29 27 26 28 30 32 33 76 89 63 85 51 84 56 91 80
Route #4: 61 42 44 39 38 36 35 37 40 43 41 72 71 93 96 54 81
Route #5: 69 98 88 60 78 73 79 7 6 2 4 46 8 45 5 3 1 70 100 55 68
[10]:
cost = result.cost() / 10
gap = 100 * (cost - BKS["cost"]) / BKS["cost"]
print(f"Found a solution with cost: {cost}.")
print(f"This is {gap:.1f}% worse than the optimal solution,", end=" ")
print(f"which is {BKS['cost']}.")
Found a solution with cost: 781.2.
This is 0.7% worse than the optimal solution, which is 776.1.
We’ve managed to find the optimal solution in a few seconds!
[11]:
fig = plt.figure(figsize=(15, 9))
plot_result(result, INSTANCE, fig)
fig.tight_layout()
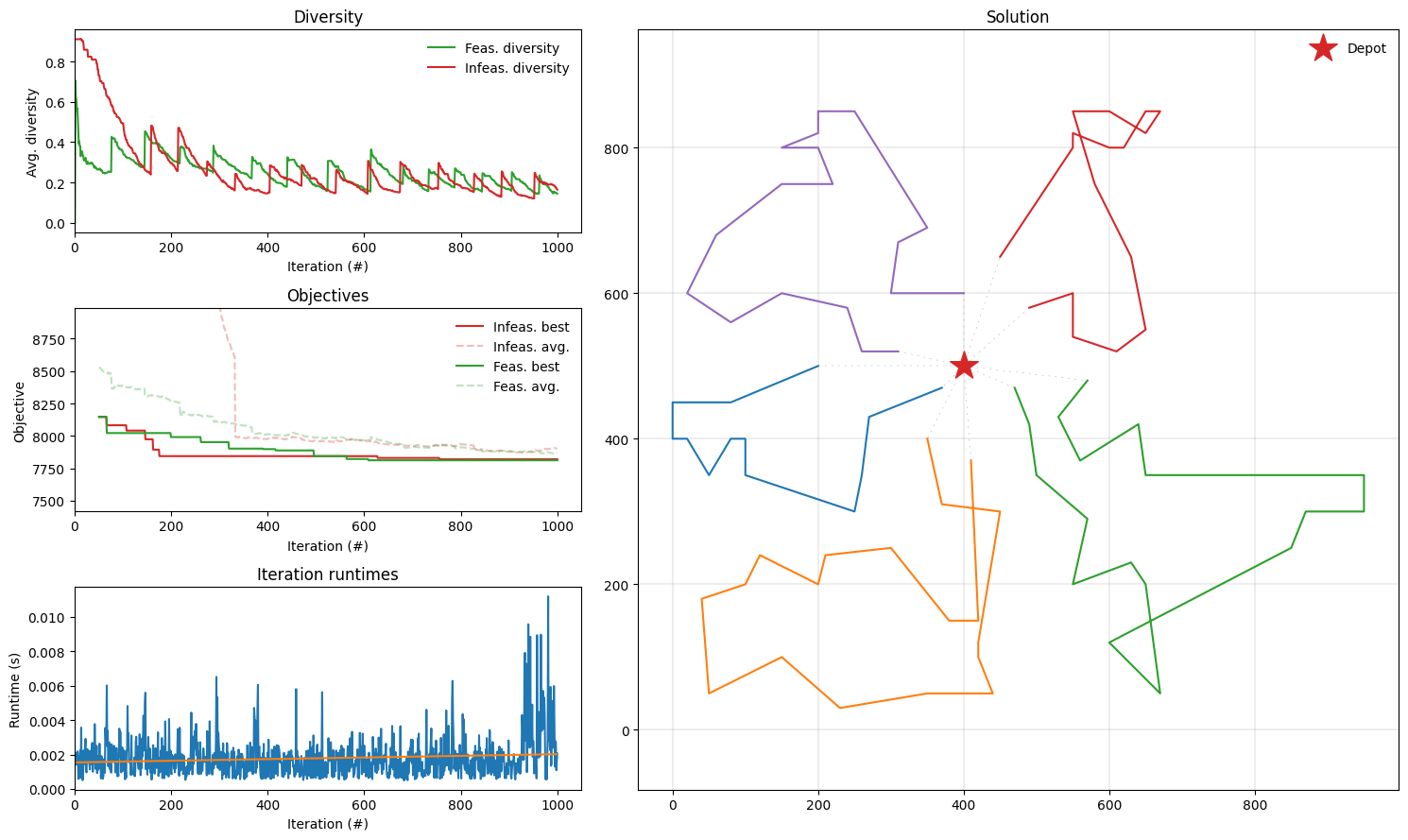
We can also inspect some statistics of the different routes, such as route distance, various durations, the number of stops and total demand.
[12]:
solution = result.best
routes = solution.get_routes()
data = [
{
"num_stops": len(route),
"distance": route.distance(),
"service_duration": route.service_duration(),
"wait_duration": route.wait_duration(),
"time_warp": route.time_warp(),
"demand": route.demand(),
}
for route in solution.get_routes()
]
header = list(data[0].keys())
rows = [datum.values() for datum in data]
tabulate(rows, header, tablefmt="html")
[12]:
| num_stops | distance | service_duration | wait_duration | time_warp | demand |
|---|---|---|---|---|---|
| 15 | 1103 | 1500 | 0 | 0 | 238 |
| 23 | 1941 | 2300 | 0 | 0 | 432 |
| 24 | 1983 | 2400 | 0 | 0 | 381 |
| 17 | 1325 | 1700 | 0 | 0 | 286 |
| 21 | 1460 | 2100 | 0 | 0 | 387 |
We can inspect the routes in more detail using the plot_route_schedule function. This will plot distance on the x-axis, and time on the y-axis, separating actual travel/driving time from waiting and service time. The clients visited are plotted as grey vertical bars indicating their time windows. We can see a jump to the start of the time window in the main (earliest) time line when a vehicle arrives early at a customer and has to wait. In some cases, there is slack in the route indicated by
a semi-transparent region on top of the earliest time line. The grey background indicates the remaining load of the truck during the route, where the (right) y-axis ends at the vehicle capacity.
[13]:
fig, axarr = plt.subplots(2, 2, figsize=(15, 9))
for idx, (ax, route) in enumerate(zip(axarr.reshape(-1), routes)):
plot_route_schedule(
INSTANCE,
route,
title=f"Route {idx}",
ax=ax,
legend=idx == 0,
)
fig.tight_layout()
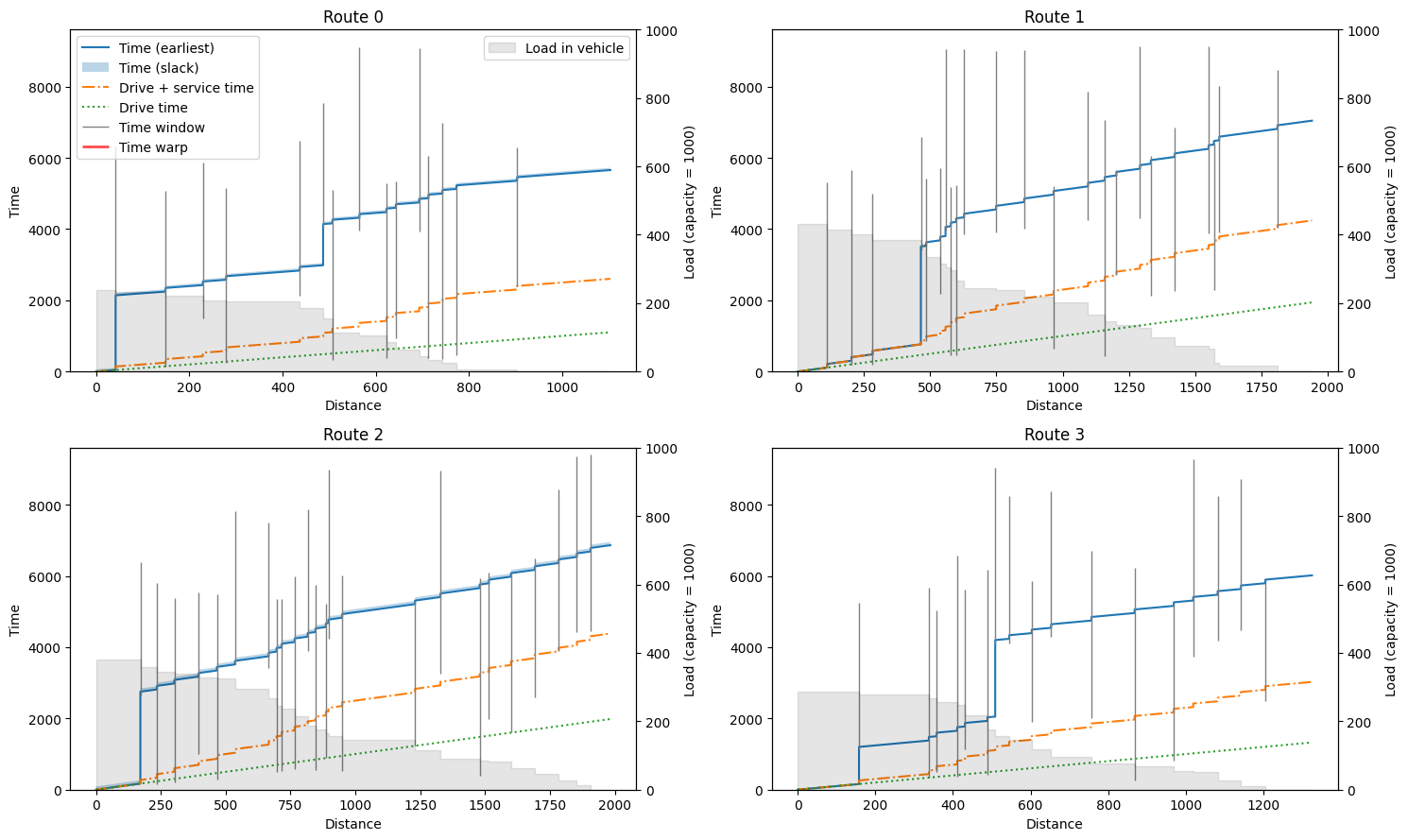
Solving a larger VRPTW instance¶
To show that PyVRP can also handle much larger instances, we will solve one of the largest Gehring and Homberger VRPTW benchmark instances. The selected instance - RC2_10_5 - has 1000 clients.
[14]:
INSTANCE = read(
"data/RC2_10_5.vrp",
instance_format="solomon",
round_func="trunc1",
)
BKS = read_solution("data/RC2_10_5.sol")
[15]:
fig = plt.figure(figsize=(15, 9))
plot_instance(INSTANCE, fig)
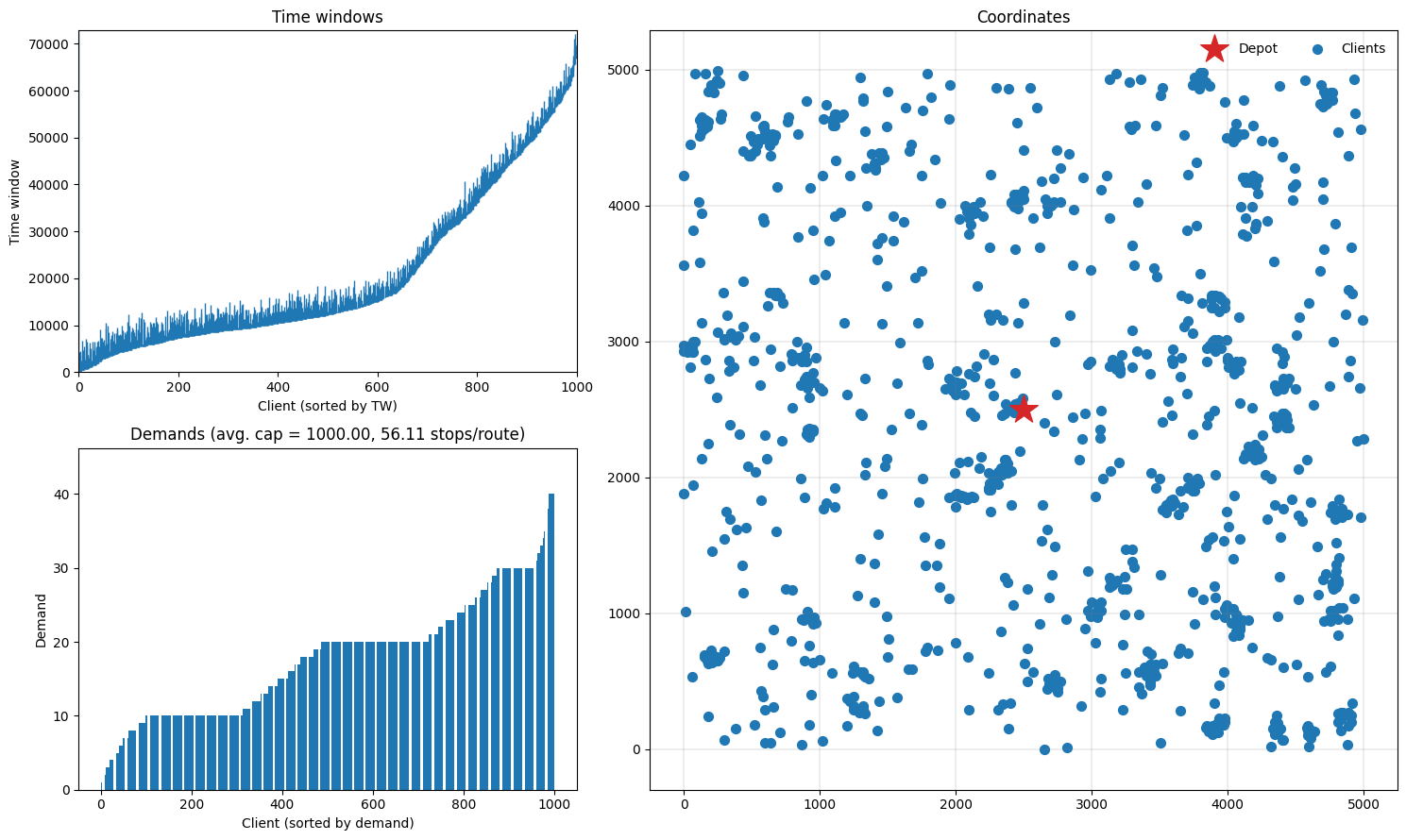
Here, we will use a runtime-based stopping criterion: we give the solver 30 seconds to compute.
[16]:
model = Model.from_data(INSTANCE)
result = model.solve(stop=MaxRuntime(30), seed=42)
[17]:
cost = result.cost() / 10
gap = 100 * (cost - BKS["cost"]) / BKS["cost"]
print(f"Found a solution with cost: {cost}.")
print(f"This is {gap:.1f}% worse than the best-known solution,", end=" ")
print(f"which is {BKS['cost']}.")
Found a solution with cost: 27835.2.
This is 7.9% worse than the best-known solution, which is 25797.5.
[18]:
plot_result(result, INSTANCE)
plt.tight_layout()
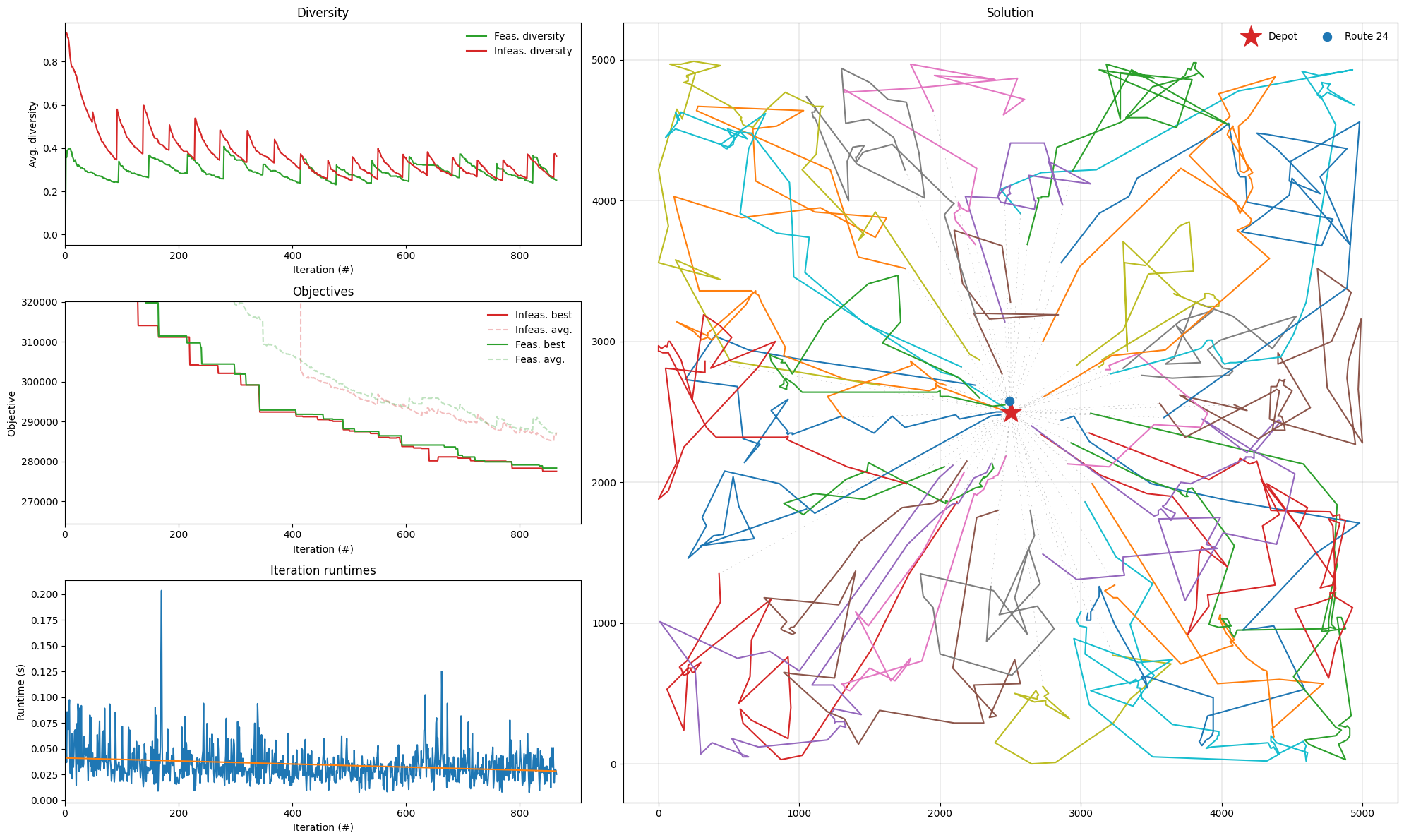
Conclusion¶
In this notebook, we used PyVRP’s Model interface to solve a CVRP instance with 438 clients to near-optimality, as well as several VRPTW instances, including a large 1000 client instance. Moreover, we demonstrated how to use the plotting tools to visualise the instance and statistics collected during the search procedure.